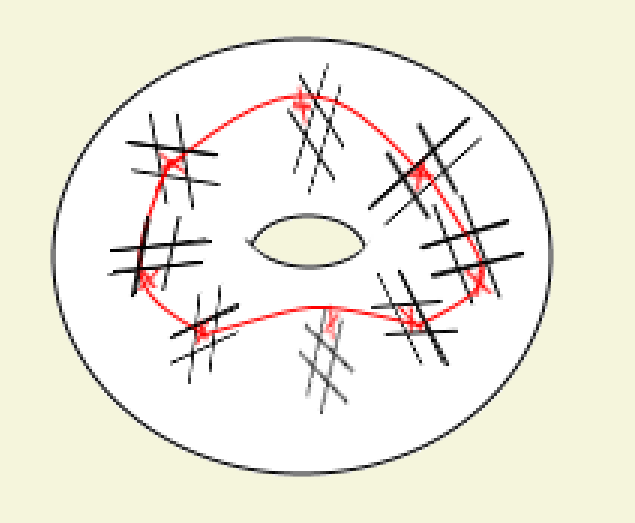
The game is played on a board of 6, 8 or 12 Tic-tac-toe grids in some circular formation, though any composite number of grids will do.
The goal of the game is to be the first to produce a "loop" of game pieces.
A loop consists of an equally-spaced ordering of the grids which returns to the first grid, along with an equally-spaced pattern going through the Tic-tac-toe grids which returns to its initial position at the first grid Consider the 8-grid boards below; the first image shows two possible orderings of boards (in this case any pattern using the second ordering might be equivalent to the first ordering), the second image shows three possible winning loops using the first ordering, and the third image shows the patterns.
A pattern can not be as long as the number of boards. Playing with or without the rule that patterns must be equally-spaced will yield differing possibilities for loops, and so equally-space patterns can be thought of as an optional rule. Further Analysis: The length of a pattern has to be divisible by the number of boards for the fastest winning loop.
If the length of the pattern is coprime with the number of boards, the loop would need to traverse the grids multiple times according to the length of the pattern.
However, this longer loop will have as many smaller winning loops as the length of the pattern.
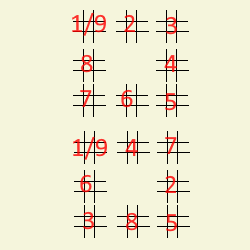
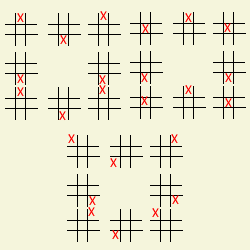
This game could probably be analysed using modulo arithmetic, the equidistribution theorem and number theory, but I do not know enough number theory.
